

Quaternion là một công cụ mạnh mẽ và hiệu quả để xử lý phép quay trong không gian ba chiều, đặc biệt là trong đồ họa máy tính, mô phỏng, và các ứng dụng cần tính toán chính xác với góc quay.
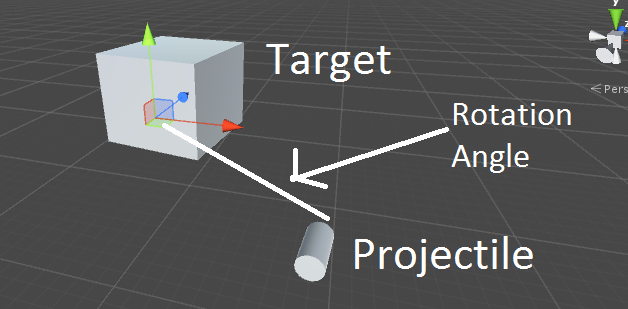
Phép quay (rotation) trong không gian 3D có thể được mô tả bằng nhiều cách, trong đó phương pháp sử dụng quaternion là một trong những cách hiệu quả nhất, đặc biệt trong các ứng dụng đồ họa máy tính và mô phỏng. Quaternion là một dạng số phức mở rộng, có thể mô tả phép quay mà không gặp phải vấn đề như góc quay gimbal lock (khóa góc quay).
1.Tại sao Unity sử dụng Quaternion thay vì Euler?
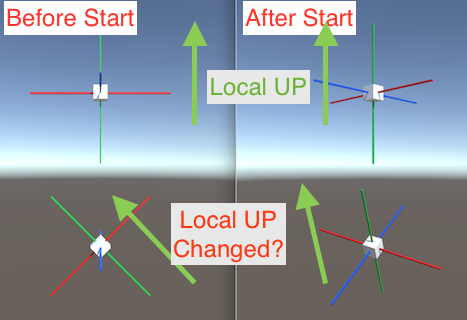
Gimbal Lock: Với hệ tọa độ Euler (gồm ba góc quay: pitch, yaw, roll), một vấn đề thường gặp là gimbal lock. Khi hai trục quay thẳng hàng, bạn sẽ mất đi một độ tự do trong việc quay, khiến việc điều khiển và tính toán trở nên khó khăn và không chính xác. Quaternion giải quyết vấn đề này vì nó không sử dụng các trục quay theo cách như Euler.
Hiệu suất cao hơn: Việc tính toán với quaternion nhanh và hiệu quả hơn so với các phép toán liên quan đến ma trận hay góc Euler. Unity có thể thực hiện các phép quay nhanh chóng mà không cần phải tính toán nhiều góc quay hay ma trận chuyển đổi phức tạp.
Dễ dàng kết hợp các phép quay: Một trong những đặc điểm mạnh mẽ của quaternion là bạn có thể kết hợp nhiều phép quay bằng cách nhân các quaternion lại với nhau. Điều này rất hữu ích khi bạn muốn áp dụng một loạt các phép quay liên tiếp. Trong khi đó, việc kết hợp các góc Euler đòi hỏi phải thực hiện thêm các phép toán phức tạp để cộng các góc.
2. Trong quá trình xử lý quay trong không gian 3D, đừng bỏ qua:
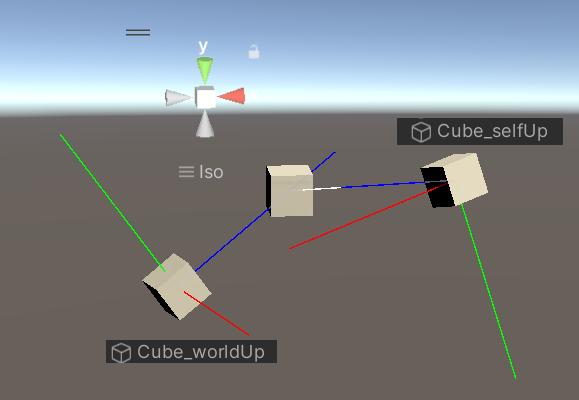
Quay một vật bằng Quaternion: Quaternion là một cách hiệu quả để đại diện cho phép quay, trong đó độ lớn của quaternion thể hiện góc quay và hướng của nó là trục quay. Nó giúp quay một vật mà không gặp phải vấn đề như gimbal lock (khóa gimbal) khi sử dụng góc Euler.
Thực hiện 2 phép quay liên tiếp (dùng toán tử *): Khi bạn muốn thực hiện hai phép quay liên tiếp, bạn có thể nhân hai quaternion lại với nhau. Toán tử * trong Unity sẽ nhân hai quaternion lại để tạo ra một quaternion mới đại diện cho phép quay tổng hợp.
Thực hiện phép quay ngược lại (dùng hàm Invert): Để quay ngược lại hoặc tìm quaternion đối nghịch (nghịch đảo), bạn có thể sử dụng hàm Invert. Điều này có nghĩa là nếu bạn đã áp dụng một phép quay cho một đối tượng, bạn có thể sử dụng hàm này để quay ngược lại.
Quay một vector theo hướng cụ thể (nhân quaternion với vector): Để quay một vector trong không gian theo một hướng xác định, bạn có thể nhân một quaternion với vector đó. Trong Unity, điều này được thực hiện bằng cách nhân quaternion với một vector 3D.
Sử dụng quaternion trong Unity giúp bạn thực hiện các phép quay một cách dễ dàng, chính xác và hiệu quả mà không gặp phải những vấn đề phức tạp liên quan đến các hệ tọa độ Euler hay ma trận quay.
Nếu như bạn là một người yêu thích và có khả năng trong việc phát triển game với các tính năng sống động, hãy gia nhập đội ngũ của SAVA META. Với môi trường làm việc sáng tạo, với đội ngũ chuyên gia hàng đầu trong ngành, bạn có thể khám phá một môi trường làm việc chuyên nghiệp, sáng tạo.
SAVA META đang là nhà phát triển hàng đầu về giải pháp nền tảng Metaverse ứng dụng công nghệ VR và game studio cho các dòng game mobile casual. Sứ mệnh của SAVA chính là mang đến những trải nghiệm chưa từng có cho cộng đồng thông qua các dự án.
Ngoài việc cung cấp môi trường làm việc chuyên nghiệp với các chuyên gia, đến với SAVA, chúng tôi còn rất nhiều các hoạt động để nâng cao chất lượng làm việc, văn hoá nội bộ mà ít công ty nào có thể làm được. Với SAVA, sự kết nối cũng như tương tác trong quá trình làm việc và trải nghiệm một môi trường làm việc tốt chính là giá trị mà chúng tôi muốn mang lại cho nhân sự của công ty.
***Tham khảo các vị trí đang tuyển dụng tại: https://savameta.com/vi/tuyen-dung