

Quaternions are a powerful and efficient tool for handling rotations in 3D space, widely utilized in computer graphics, simulations, and applications requiring precise rotation calculations.
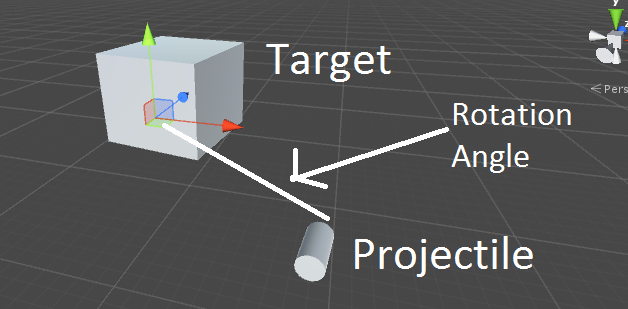
1.Why Use Quaternions in Unity Instead of Euler Angles?
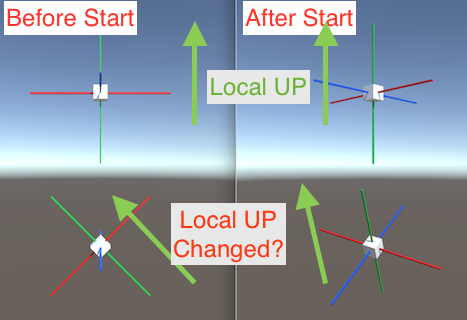
1.1 Avoiding Gimbal Lock:
Euler angles, defined by three rotational axes (pitch, yaw, roll), can encounter the problem of gimbal lock, where two rotational axes align, causing the loss of one degree of freedom. Quaternions solve this issue by representing rotations without relying on such axes.
1.2 Higher Efficiency:
Quaternion calculations are faster and more computationally efficient than matrix transformations or Euler angles, allowing Unity to handle rotations quickly without complex conversions or additional calculations.
1.3 Combining Rotations:
Quaternions allow seamless combination of multiple rotations by simply multiplying them. This is particularly useful for applying consecutive rotations in Unity, whereas combining Euler angles requires more intricate transformations.
2. Key Use Cases for Quaternions in Unity
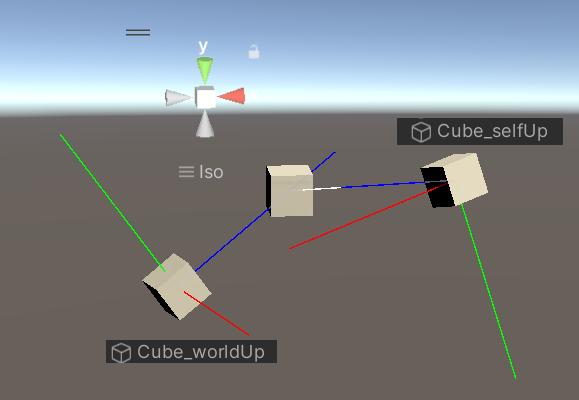
2.1 Rotating Objects with Quaternions:
Quaternions represent rotations in a way where their magnitude indicates the rotation angle, and their direction defines the rotation axis. This approach avoids gimbal lock, ensuring smooth and accurate rotations.
2.2 Sequential Rotations Using the * Operator:
To perform consecutive rotations, multiply two quaternions using Unity’s * operator. This results in a new quaternion representing the combined rotation.
2.3 Reversing a Rotation Using Quaternion.Inverse:
To reverse or negate a rotation, use Quaternion.Inverse. This is useful when undoing a rotation applied to an object or determining an opposite orientation.
2.4 Rotating Vectors with Quaternions:
To rotate a vector in space, multiply the vector by a quaternion. Unity provides a straightforward method to accomplish this with a combination of quaternion and vector multiplication, resulting in precise directional changes.
3. Benefits of Using Quaternions in Unity
3.1 Accuracy and Stability:
Quaternions ensure rotations are calculated without precision loss or instability, critical in high-performance applications like games or simulations.
3.2 Simplified Transformations:
Unity’s quaternion system simplifies complex transformations, saving time and reducing the risk of errors.
3.3 Flexibility in Motion Control:
By providing straightforward tools for combining, reversing, and manipulating rotations, Unity empowers developers to create dynamic and natural movements effortlessly.
If you are passionate about creating immersive, dynamic features for games and have expertise in utilizing advanced tools like quaternions, SAVA META offers an ideal platform to grow your career.
As a leading developer in Metaverse solutions and casual mobile games, SAVA META is dedicated to delivering unprecedented experiences to the gaming community.
Join us to work in a professional, creative environment alongside industry experts. At SAVA META, we value collaboration, innovation, and building a thriving culture that inspires success.
Explore career opportunities at: https://savameta.com/c-careers